Как посчитать MaxPain на пальцах?

---

В 2004 году в опционной торговле появилась теория, согласно которой цена того или иного актива стремится к некому "волшебному" уровню, называемому уровнем Max Pain ( если дословно, то уровнем максимальной боли). Такое название небезосновательно, ибо отражает тот факт, что, если цена на момент экспирации опционного контракта будет находиться именно у  этого уровня, то держатели опционов понесут максимально возможные убытки. А продавцы опционов напротив будут чувствовать себя очень комфортно.

В данной статье я не буду вдаваться в подробности данной теории, так как подобной информации достаточно много в сети, и при желании каждый может самостоятельно найти нужные статьи и обстоятельно  разобраться в этой теме. Я же хочу рассказать немного о том, как же рассчитывается этот MaxPain. Меня достаточно часто об этом спрашивают, сетуя на то, что в сети нет об этом адекватной информации на русском языке.

Итак, давайте же не будем тянуть время и на конкретном примере рассчитаем MaxPain. Возьмем следующие исходные данные:

   1. Дата  28.09.2018г.
   2. Базовый актив - фьючерс 6EZ8
   3. Опционный контракт - EUUV8 (в программе Options Trader это EUU-OCT18)

 
Допустим, что фьючерс 6EZ8 на момент экспирации опциона EUUV8 имеет цену 1,1700. Тогда:

PUT -опционы на страйке 1,1700 и ниже не имеют никакой внутренней стоимости(вне денег).
PUT -опцион на страйке 1,1750 имеет внутреннюю стоимость 50 пунктов (1,1750 – 1,1700), так как держатель put -опциона в момент экспирации может купить фьючерс по рыночной цене 1,1700 и тут же продать его по цене 1,1750 ( такое право даёт опционный контракт) и в итоге останется в прибыли размером в 50 пунктов.
PUT -опцион на страйке 1,1800 имеет внутреннюю стоимость 100  пунктов (1,1800 – 1,1700)
PUT -опцион на страйке 1,1850 имеет внутреннюю стоимость 150 пунктов (1,1850 – 1,1700)
и т.д.  – внутренняя стоимость увеличивается на шаг страйка (т.е. на 50 пунктов в данном случае)
 

Аналогично и для CALL- опционов, только в обратную сторону:
CALL-опционы на страйке 1,1700 и выше не имеют никакой внутренней ценности.
CALL-опцион на страйке 1,1650 имеет внутреннюю стоимость 50  пунктов (1,1700-1,1650), так как держатель call-опциона вправе купить фьючерс в момент экспирации по цене 1,1650 (такое право даёт опционный контракт) и тут же продать его по рыночной цене 1,1700, и в итоге останется в прибыли размером в 50  пунктов .
CALL-опцион на страйке 1,1600 имеет внутреннюю стоимость 100  пунктов (1,1700-1,1600)
CALL-опцион на страйке 1,1550 имеет внутреннюю стоимость 1 50 пунктов(1,1700-1,1550)
и т.д.  – внутренняя стоимость увеличивается на шаг страйка (т.е. на 50 пунктов в данном случае)

 
Берём всю серию страйков (сморите таблицу ниже - столбец   Strike )  по данному контракту и высчитываем значение внутренней стоимости  (в таблице это столбцы – Intristic Call и Intristic Put соответственно) по каждому страйку для цены базового актива, равную   1,1700 ( столбец Price )

Для тех, кто будет проверять этот пример в Excel при условии размещения таблицы в левом верхнем углу рабочего листа, формула для столбца Intristic Call имеет вид =ЕСЛИ(A2-B2>0;A2-B2;0) , а для столбца Intristic Put - =ЕСЛИ(B2-A2>0;B2-A2;0)

 
Далее берём размер ОИ на страйках по CALL - опционам (столбец   Call OI ) и путём умножения ОИ на внутреннюю стоимость, которую мы уже определили в столбце Intristic Call ,  находим сначала общую стоимость ( столбец   Тotoal Call )   для каждого страйка, а потом  - путем суммирования найденных значений и  общую стоимость по всем страйкам ( внизу таблицы итоговое значение - 105). Формула Excel для столбца Тotoal Call имеет вид =E2*C2


Выполняем аналогичную операцию  и для   PUT- опционов. Формула Excel для столбца Тotoal Put имеет вид =G3*D3


Последним шагом является суммирование общей стоимости по всем страйкам для PUT и CALL . В примере это 233=105+128

Price	Strike	Intristic Call	Inristic Put	Call OI	Total Call	Put OI	Total Put
1,1700	0,9950	0,1750	0,0000	0	0	34	0
1,1700	1,0000	0,1700	0,0000	0	0	93	0
1,1700	1,0050	0,1650	0,0000	0	0	17	0
1,1700	1,0100	0,1600	0,0000	0	0	183	0
1,1700	1,0150	0,1550	0,0000	0	0	39	0
1,1700	1,0200	0,1500	0,0000	1	0,15	72	0
1,1700	1,0250	0,1450	0,0000	2	0,29	34	0
1,1700	1,0300	0,1400	0,0000	3	0,42	40	0
1,1700	1,0350	0,1350	0,0000	15	2,025	88	0
1,1700	1,0400	0,1300	0,0000	3	0,39	204	0
1,1700	1,0450	0,1250	0,0000	9	1,125	122	0
1,1700	1,0500	0,1200	0,0000	22	2,64	579	0
1,1700	1,0550	0,1150	0,0000	11	1,265	75	0
1,1700	1,0600	0,1100	0,0000	11	1,21	330	0
1,1700	1,0650	0,1050	0,0000	6	0,63	97	0
1,1700	1,0700	0,1000	0,0000	12	1,2	363	0
1,1700	1,0750	0,0950	0,0000	29	2,755	585	0
1,1700	1,0800	0,0900	0,0000	22	1,98	359	0
1,1700	1,0850	0,0850	0,0000	15	1,275	437	0
1,1700	1,0900	0,0800	0,0000	51	4,08	633	0
1,1700	1,0950	0,0750	0,0000	28	2,1	582	0
1,1700	1,1000	0,0700	0,0000	33	2,31	3172	0
1,1700	1,1050	0,0650	0,0000	52	3,38	768	0
1,1700	1,1100	0,0600	0,0000	28	1,68	1500	0
1,1700	1,1150	0,0550	0,0000	32	1,76	1030	0
1,1700	1,1200	0,0500	0,0000	41	2,05	1454	0
1,1700	1,1250	0,0450	0,0000	19	0,855	1365	0
1,1700	1,1300	0,0400	0,0000	118	4,72	2709	0
1,1700	1,1350	0,0350	0,0000	264	9,24	2925	0
1,1700	1,1400	0,0300	0,0000	429	12,87	2988	0
1,1700	1,1450	0,0250	0,0000	260	6,5	2774	0
1,1700	1,1500	0,0200	0,0000	565	11,3	3256	0
1,1700	1,1550	0,0150	0,0000	494	7,41	3757	0
1,1700	1,1600	0,0100	0,0000	867	8,67	5131	0
1,1700	1,1650	0,0050	0,0000	1729	8,645	4373	0
1,1700	1,1700	0,0000	0,0000	3067	0	2443	0
1,1700	1,1750	0,0000	0,0050	3067	0	2134	10,67
1,1700	1,1800	0,0000	0,0100	3014	0	1659	16,59
1,1700	1,1850	0,0000	0,0150	3133	0	1314	19,71
1,1700	1,1900	0,0000	0,0200	4586	0	1060	21,2
1,1700	1,1950	0,0000	0,0250	3324	0	213	5,325
1,1700	1,2000	0,0000	0,0300	3403	0	210	6,3
1,1700	1,2050	0,0000	0,0350	1339	0	113	3,955
1,1700	1,2100	0,0000	0,0400	1444	0	55	2,2
1,1700	1,2150	0,0000	0,0450	676	0	95	4,275
1,1700	1,2200	0,0000	0,0500	1043	0	95	4,75
1,1700	1,2250	0,0000	0,0550	303	0	11	0,605
1,1700	1,2300	0,0000	0,0600	470	0	22	1,32
1,1700	1,2350	0,0000	0,0650	1412	0	11	0,715
1,1700	1,2400	0,0000	0,0700	410	0	3	0,21
1,1700	1,2450	0,0000	0,0750	500	0	10	0,75
1,1700	1,2500	0,0000	0,0800	710	0	11	0,88
1,1700	1,2550	0,0000	0,0850	383	0	6	0,51
1,1700	1,2600	0,0000	0,0900	265	0	32	2,88
1,1700	1,2650	0,0000	0,0950	126	0	15	1,425
1,1700	1,2700	0,0000	0,1000	78	0	69	6,9
1,1700	1,2750	0,0000	0,1050	90	0	67	7,035
1,1700	1,2800	0,0000	0,1100	249	0	54	5,94
1,1700	1,2850	0,0000	0,1150	97	0	10	1,15
1,1700	1,2900	0,0000	0,1200	131	0	3	0,36
1,1700	1,2950	0,0000	0,1250	18	0	2	0,25
1,1700	1,3000	0,0000	0,1300	246	0	2	0,26
1,1700	1,3050	0,0000	0,1350	65	0	2	0,27
1,1700	1,3100	0,0000	0,1400	26	0	2	0,28
1,1700	1,3150	0,0000	0,1450	18	0	3	0,435
1,1700	1,3200	0,0000	0,1500	221	0	3	0,45
1,1700	1,3250	0,0000	0,1550	16	0	2	0,31
1,1700	1,3300	0,0000	0,1600	2	0	0	0
1,1700	1,3350	0,0000	0,1650	1	0	0	0
1,1700	1,3400	0,0000	0,1700	0	0	0	0
1,1700	1,3450	0,0000	0,1750	7	0	0	0
1,1700	1,3500	0,0000	0,1800	5	0	0	0
1,1700	1,3550	0,0000	0,1850	33	0	0	0
1,1700	1,3600	0,0000	0,1900	0	0	0	0
1,1700	1,3650	0,0000	0,1950	0	0	0	0
1,1700	1,3700	0,0000	0,2000	0	0	0	0
1,1700	1,3750	0,0000	0,2050	0	0	0	0
1,1700	1,3800	0,0000	0,2100	0	0	0	0
1,1700	1,3850	0,0000	0,2150	0	0	0	0
1,1700	1,3900	0,0000	0,2200	0	0	0	0
1,1700	1,3950	0,0000	0,2250	0	0	0	0
1,1700	1,4000	0,0000	0,2300	0	0	0	0
1,1700	1,4050	0,0000	0,2350	0	0	0	0
				ИТОГО:	105		128
							233

 

Теперь заглянем во всем известную платформу "Квик-страйк" и посмотрим, правильно ли мы всё посчитали? И, о чудо, всё верно.

 

 

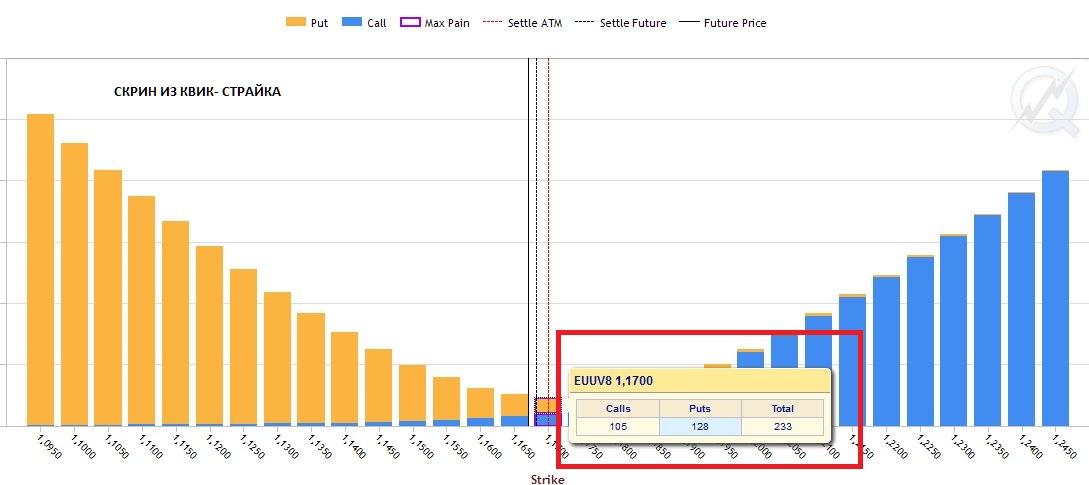
Расчёт, указанный выше,  необходимо сделать для нескольких цен фьючерса, равных страйкам. Т.е.  условно говоря, составить несколько таблиц  для  цен фьючерса, начиная от  цены актива 0,9950 до цены 1,4050.

Для упрощения  можно сузить диапазон от текущей цены на несколько шагов туда и обратно (например  от 1,1700 - 4 шага вниз и вверх) - тогда нужно будет составить всего 9 таблиц:

Таблица 1 - для цены актива  1,1500
Таблица 2 - для цены актива  1,1550
Таблица 3 - для цены актива  1,1600
Таблица 4 - для цены актива  1,1650
Таблица 5 - для цены актива  1,1700 (это наша таблица)
Таблица 6 - для цены актива  1,1750
Таблица 7 - для цены актива  1,1800
Таблица 8 - для цены актива  1,1850
Таблица 9 - для цены актива  1,1900

Всё это можно сделать, конечно,  более компактно и, вообще, программно, но здесь всё изложено на "пальцах" для понятности и наглядности.

Из каждой таблицы мы будем иметь значение общей стоимости (это 233 для цены актива 1,17 из таблицы 5, которая как раз в данной статье).

Наименьшее значение этой общей стоимости из всех найденных как раз и является уровнем MaxPain.  В рассматриваемом случае (для этого контракта на эту дату) это уровень 1,1700, так как именно на этом уровне наименьшее значение стоимости = 233)

 

Вот! И ничего сложного!

На этом пока всё. До встречи.

 

P.S. В программе Options Trader показатель Max Pain пока не рассчитывается, но в последующих версиях будет обязательно включен.

---